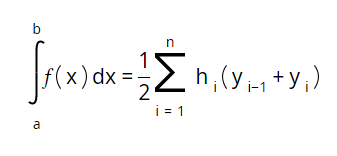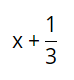Welcome

formula_tor is a small JS library that visualizes mathematical expressions into the HTML markup. Live demo.

Install & Setup

If your project uses NPM:

npm i @zaba-web/formula_tor

and then in your project file:

import Formulator from '@zaba-web/formula_tor'

Otherwise, you can use CDN:

<script src='https://cdn.jsdelivr.net/npm/@zaba-web/formula_tor/dist/formulator.js'></script>

Then, if you want to save visualized markup somewhere and use it later, you need to add file with styles on that page:

import '@zaba-web/formula_tor/dist/style.css'

Or with CDN:

<link refl='stylesheet' href='https://cdn.jsdelivr.net/npm/@zaba-web/formula_tor/dist/style.css'>

Usage

Getting started

First of all, we need to create an HTML element that we will use as a container for formula.

<div class='formula-container'></div>

Then we need to create instance of Formulator class. Formulator's constructor requires container (HTML element) as the argument.

const containerElement = document.querySelector('.formula-container')
const formulator = new Formulator(containerElement)

That's it. Now we can visualize formulas by call formulator.visualize(expressionString) method.

For example, formulator.visualize('x + 1/3') will produce following:

Usage principles

There are several types of parts from which we build expression:

• Regular Strings

Regular string is a character or sequence of characters that are not operators or functions (see Operators table and Functions table).

Example: 10x + 4 - 8 = 15

(Note: formula_tor's visualizer considers +, -, =, *, <, > and | as regular strings because it doest not chagne a view of formula in terms of markup)

• Operators

Operators are reserved characters (see Operators table) that works with operands. There are unary operators that work with single operand and binary that work with two respectively.

As an operand you can use arbitary expression. If this expression consists more than from one regular string or it is another operator or function, it should be wrapped in parentheses.

Exampe 1: 1/5 - binary operator / with two operands: 1 and 2. Both of them are regular string

Example 2: 1/(2+2*x) - in this example we use more than one regular string.

Example 3: 1/(2/5) - in this example we use another binary operator as an operand.

• Functions

Functions are reserved words that work with arguments (see Functions table). Name of function begins with capital letter. Arguments should be written in parentheses, separated by coma (,) character.

To the function's arguments applied the same rules as for operands. If you intend to use function as an operand or argument of another function you should wrap it in parentheses.

Example 1: Root(x, 3)

Example 2: 1/(Root(x, 3))

Example 3: Root((1/3x), 3)

Example 4: Root((Root(2,3)),2)

• Constants

There are several most common used math symbols that are factored as constants (see Constants table). Constant name should be written in capital letters.

• Separation

Commonly, parts of the formula separates automatically. But if you are using two parts of formula without explicit seprator (Operators and +, -, =, *, <, >, (, ), | characters) you should separate it by hand using coma separator.

Example 1: DELTA, x

Example 1: 3, Root(4, 2)

Operatos table

Operator	Description	Count of operands	Usage example
^	Power operator	1	x^2
_	Bottom index	1	x_i
/	Division operator	2	1/2

Functions table

Function	Description	Count of agrumetns	Usage example
Root(expr, nth_root)	Root construction visualization	2	Root(27, 3)
Log(expr, base)	Log function	2	Log(x, 2) = 4
System2(expr1, expr2)	System of 2 equations/inequalities	2	System2((2+xy = 2), (y - x = 4))
System3(expr1, expr2, expr3)	System of 3 equations/inequalities	3	System3((2+xy = 2), (y - x = 4), (y - x = 4))
System4(expr1, expr2, expr3, expr4)	System of 4 equations/inequalities	4	System4((2+xy = 2), (y - x = 4), (y - x = 4), (y - x = 4))
IndefInt(expr)	Indefinite Integral	1	IndefInt((1/dx))
DefInt(expr, from, to)	Definite Integral	3	DefInt((1/dx), 0, PI)
IntLine(from, to)	Using in definite integral calculation	2	IntLine(0, 1)
Lim(expr, variable, approaching)	Limit visualization	3	Lim((x^a,lnx), x, 0)
Indexes(topIndexExpr, bottomIndexExpr)	Put two indexes togather	2	x, Indexes(2,i)
Sum(expr, topExp, bottomExpr)	Visualize sum	3	Sum((x_i+2), m, (i=1))
Vec(expr)	Add vetor arrow to expression	1	Vec(A)

Constants table

Constant	Character
ALPHA	α
BETA	β
GAMMA	γ
DELTA	Δ
DELTASM	δ
PI	π
PHI	φ
DEG	°
INFINITY	∞